Synthèse du cours
Plans d’échantillonnage et d’expérience
Échantillonnage
- Aléatoire simple: chaque individu a la même probabilité d’être échantillonné
- Systématique: à intervalles réguliers à partir d’une origine aléatoire
- Stratifié: division de la population en strates, échantillonnage aléatoire par strate
- Par grappe: échantilonner des groupes d’individus, prendre soit tous les individus d’un groupe, soit un échantillon aléatoire simple par groupe (multistade)
Plan d’expérience
- Groupe témoin
- Assignation aléatoire des individus aux traitements
- Contrôle de la variation par des blocs
- Parcelles divisées: deuxième facteur varie à l’intérieur des réplicats du premier facteur
Structure d’un test statistique
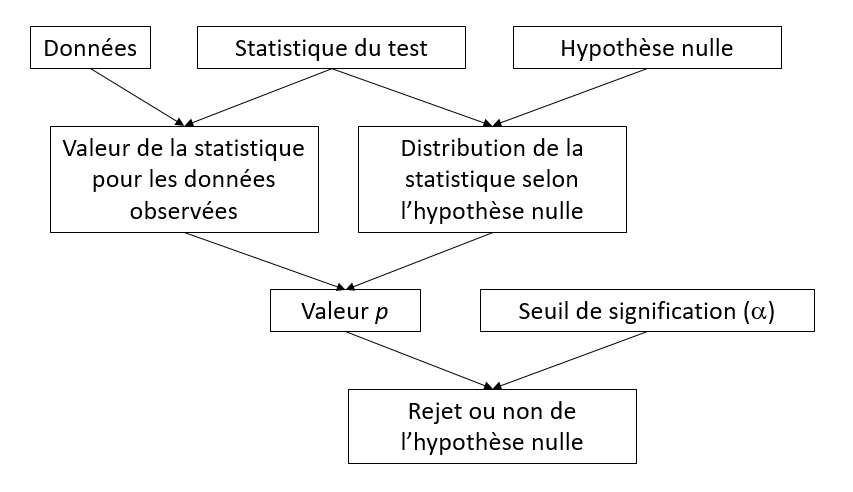
Exemples
| test \(t\) à un échantillon (\(n\) individus) | ANOVA à un facteur (\(m\) groupes de \(n\) individus) | |
|---|---|---|
| Hypothèse nulle | La moyenne \(\bar{x}\) est égale à \(\mu\) | La moyenne est la même pour les \(m\) groupes |
| Statistique | \(t = (\bar{x} - \mu) / (s/\sqrt{n})\) | \(F = MSA/MSE\) |
| Distribution | \(t\) avec \(n-1\) degrés de liberté | \(F\) avec \(m(n-1)\) et \((m - 1)\) degrés de liberté |
Points clés sur les tests d’hypothèse
Le seuil de signification est la probabilité de rejeter l’hypothèse nulle lorsqu’elle est vraie.
Il faut choisir un test et un seuil de signification avant d’analyser les résultats.
Si on effectue plusieurs test dans une expérience, la probabilité de rejeter par erreur une des hypothèses nulles augmente (problème des comparaisons multiples).
La puissance d’un test est la probabilité de rejeter l’hypothèse nulle si elle est fausse. Plus l’effet à détecter est faible par rapport à la variance de la réponse (faible ratio signal/bruit), puis \(n\) doit être élevé pour avoir la même puissance.
Avec un \(n\) suffisamment grand, même un très petit effet sera jugé statistiquement significatif; cela ne signifie pas que l’effet est important.
Estimation de paramètres
Biais: écart systématique entre l’estimé d’un paramètre et sa valeur exacte.
Erreur-type: écart-type de l’estimé d’un paramètre, dû à l’échantillonnage limité; diminue lorsque \(n\) augmente.
- Différent de l’écart-type de la réponse: mesure la variabilité entre individus, ne dépend pas de \(n\).
Intervalle de confiance: Dans X% des échantillons possibles, l’intervalle de confiance à X% de l’estimé d’un paramètre contient la vraie valeur de ce paramètre.
Relation entre intervalle de confiance et test d’hypothèse: l’hypothèse \(\theta = \theta_0\) peut être rejetée à un seuil \(\alpha\) si l’intervalle de confiance à \(100\%(1 - \alpha)\) de \(\hat{\theta}\) n’inclut pas \(\theta_0\).
Test de différences entre groupes
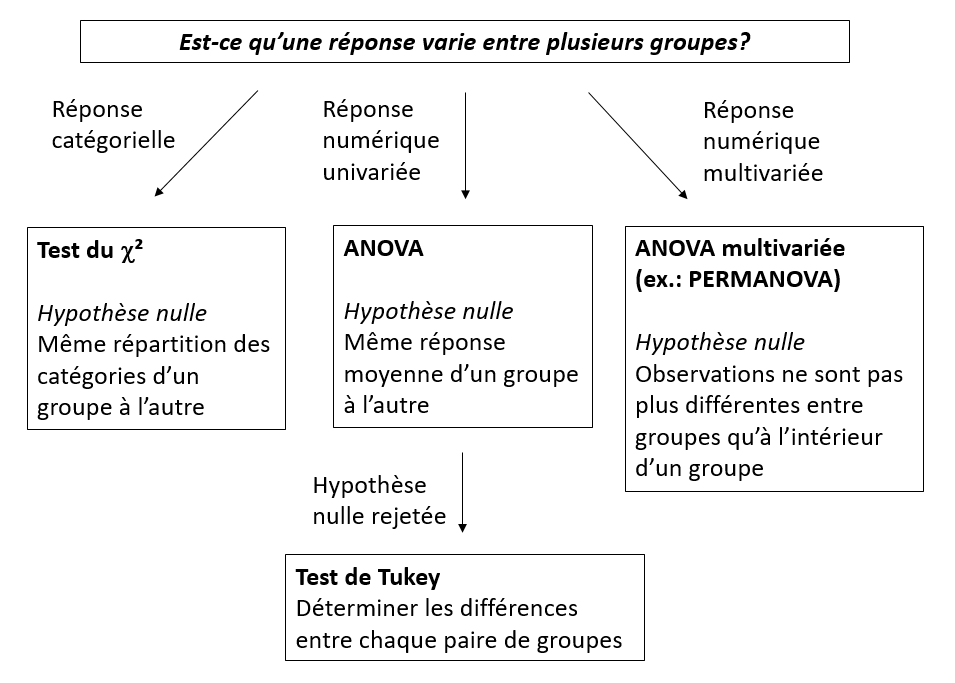
Suppositions de l’ANOVA
- Indépendance: Les observations sont indépendantes.
- Normalité: La réponse suit une distribution normale dans chaque groupe.
- Homoscédasticité: La variance est la même dans chaque groupe.
L’ANOVA tolère bien des écarts modérés par rapport à la normalité, donc cette supposition est moins critique que les deux autres.
Avec seulement 2 groupes, le test \(t\) permet des variances inégales.
Modèles de régression
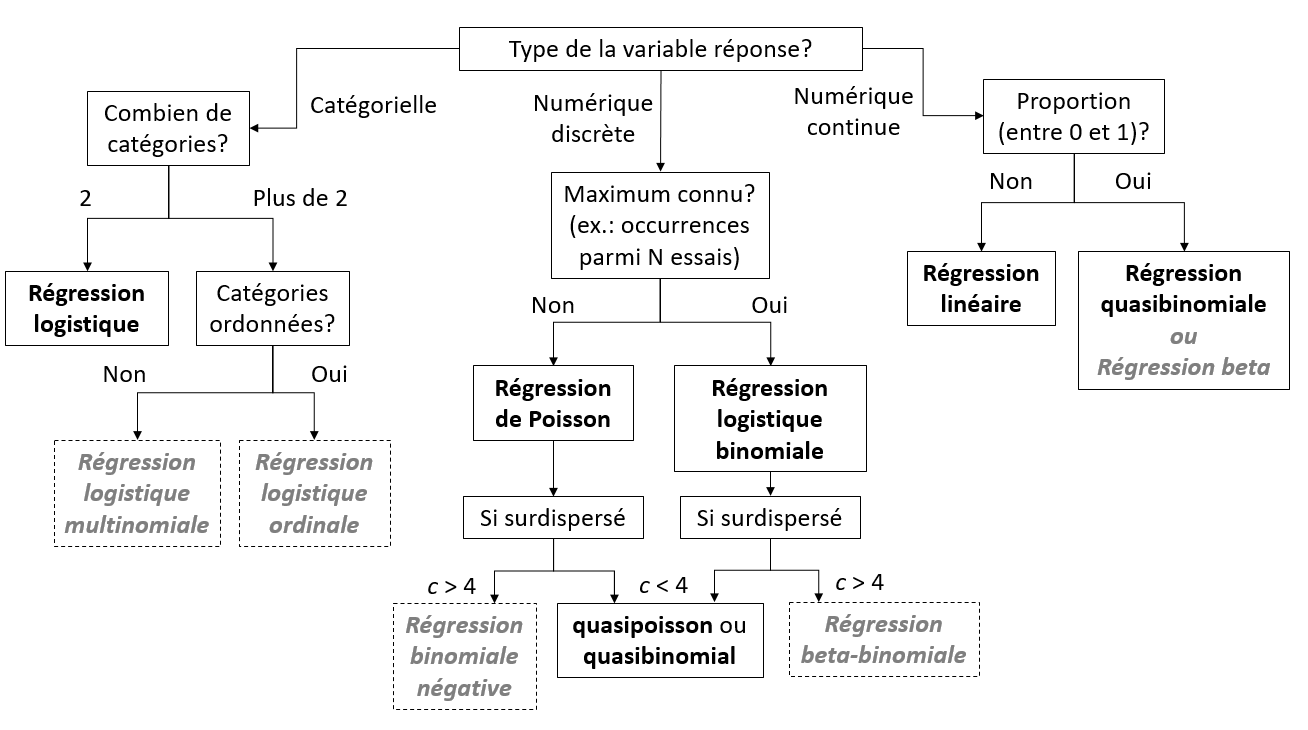
Types de modèles en gris non vus dans ce cours.
Suppositions du modèle de régression linéaire
- Effet linéaire et additif des prédicteurs sur la réponse
- Sinon: transformer la réponse et/ou les prédicteurs, inclure des interactions, modèles additifs généralisés (GAM)
- Indépendance des résidus
- Sinon: modèles mixtes (données groupées), modèles d’autocorrélation temporelle ou spatiale
- Uniformité de la variance (homoscédasticité)
- Sinon: transformer la réponse, régression linéaire pondérée
- Normalité
- Sinon: transformer la réponse (seulement si très loin de la normalité)
Modèles en italique non vus dans ce cours.
Interpréter les coefficients d’une régression
Régression linéaire sans interaction
\[ y \sim w + x + z \]
\(y\) est la réponse numérique, \(w\) et \(x\) sont des prédicteurs numériques, \(z\) est un facteur avec codage de traitement (défaut dans R) et trois niveaux: A (référence), B et C.
Coefficients estimés:
- (Intercept): Valeur moyenne de la réponse lorsque tous les prédicteurs sont à leur niveau de référence (0 pour les prédicteurs numériques).
- w: Effet sur \(y\) d’une augmentation unitaire de \(w\) si \(x\) et \(z\) restent constants.
- x: Effet sur \(y\) d’une augmentation unitaire de \(x\) si \(w\) et \(z\) restent constants.
- zB: Différence de \(y\) entre les niveaux B et A de \(z\), si \(w\) et \(x\) restent constants.
- zC: Différence de \(y\) entre les niveaux C et A de \(z\), si \(w\) et \(x\) restent constants.
Interaction entre un prédicteur numérique et un facteur
\[ y \sim x * z \]
Coefficients estimés:
- (Intercept): Même interprétation.
- x: Effet sur \(y\) d’une augmentation unitaire de \(x\) si \(z\) = A.
- zB: Différence de \(y\) entre les niveaux B et A de \(z\) si \(x\) = 0.
- zC: Différence de \(y\) entre les niveaux C et A de \(z\) si \(x\) = 0.
- x:zB: Différence entre la pente de \(y\) vs. \(x\) si \(z\) = B et cette pente si \(z\) = A.
- x:zC: Différence entre la pente de \(y\) vs. \(x\) si \(z\) = C et cette pente si \(z\) = A.
Autrement dit, il faut additionner les coefficients x et x:zB pour obtenir la pente de \(y\) vs. \(x\) si \(z\) = B.
Interaction entre deux prédicteurs numériques
\[ y \sim w * x \]
Coefficients estimés:
- (Intercept): Même interprétation.
- w: Effet sur \(y\) d’une augmentation unitaire de \(w\) si \(x\) = 0.
- x: Effet sur \(y\) d’une augmentation unitaire de \(x\) si \(w\) = 0.
- w:x: Effet sur la pente de \(y\) vs. \(x\) d’une augmentation unitaire de \(w\), OU effet sur la pente de \(y\) vs. \(w\) d’une augmentation unitaire de \(x\) (deux interprétations équivalentes).
Modèles linéaires généralisés
Dans ces modèles, la moyenne de \(y\) n’est pas égale à la combinaison linéaire des prédicteurs \(\eta\), mais à une transformation de \(\eta\) selon une fonction de lien.
L’interprétation des paramètres ci-dessus donne l’effet sur \(\eta\). Pour obtenir l’effet sur la moyenne de \(y\), il faut appliquer l’inverse de la fonction de lien.
- Inverse du lien logit: \(y = 1/(1 + \exp(- \eta))\)
- Inverse du lien log: \(y = \exp(\eta)\)
Normalisation des prédicteurs numériques
- Normaliser un prédicteur en soustrayant la moyenne et en divisant par l’écart-type.
\[ x_{norm} = \frac{x - \mu_x}{\sigma_x} \]
Puisque \(x_{norm} = 0\) correspond à la moyenne de \(x\), il est plus facile d’interpréter l’ordonnée à l’origine (intercept) dans tous les cas, et les coefficients dans le cas d’un modèle avec interactions.
Puisqu’une augmentation unitaire de \(x_{norm}\) correspond à augmenter \(x\) d’un écart-type, la magnitude du coefficient donne une idée de l’importance de l’effet de ce prédicteur. On peut ainsi comparer des prédicteurs dont les échelles originales sont différentes.
Sélection de modèles
Choix entre modèles de différentes complexités: compromis entre sous-ajustement et surajustement.
Sous-ajustement: effets importants non inclus dans le modèle.
Surajustement: le modèle reproduit très bien les données utilisées pour son ajustement, mais performe moins bien sur de nouvelles données.
En l’absence de données indépendantes pour évaluer le pouvoir prédictif de différents modèles, on peut l’estimer avec l’AIC (et ses variantes).
Points clés pour la sélection de modèles
Comparer selon la même variable réponse et les mêmes observations.
Le meilleur modèle n’est peut-être pas bon: vérifier l’ajustement.
Si plusieurs modèles sont plausibles, la moyenne pondérée de leurs prédictions est souvent meilleure que les prédictions du meilleur modèle.
Collinéarité
Problème où deux ou plusieurs prédicteurs sont fortement corrélés.
Différentes options:
- Choisir a priori quels prédicteurs éliminer, d’après notre connaissance du système.
- Utiliser l’AIC pour choisir entre différents modèles qui incluent des sous-ensembles non collinéaires des prédicteurs.
- Effectuer une ordination des prédicteurs pour obtenir des axes non corrélés, puis effectuer une régression de la réponse en fonction de ces nouvelles variables.