La méthode du bootstrap - Solutions
Données
Pour ce laboratoire, nous utiliserons le jeu de données sphagnum_cover.csv, qui provient de l’article:
Maanavilja, L., Kangas, L., Mehtätalo, L. and Tuittila, E.‐S. (2015), Rewetting of drained boreal spruce swamp forests results in rapid recovery of Sphagnum production. J Appl Ecol, 52: 1355-1363. doi:10.1111/1365-2664.12474)
Ces données contiennent des mesures du pourcentage de couverture par les sphaignes (sphcover) pour 36 marécages boréaux divisés en trois types (habitat): Dr = drainés, Re = remouillés et Un = non-drainés.
cover <- read.csv("sphagnum_cover.csv")
str(cover)## 'data.frame': 36 obs. of 3 variables:
## $ site : chr "AmLuxx" "EvLuPa" "EvLuVK" "HeLuxx" ...
## $ habitat : chr "Un" "Un" "Un" "Un" ...
## $ sphcover: num 35.3 56.2 46.6 56 54.3 ...1. Estimation de la couverture moyenne pour les marécages drainés
- À partir du jeu de données, faites l’extraction des valeurs de sphcover pour les marécages drainés. Calculez le pourcentage de couverture moyen, ainsi que son erreur-type selon la formule classique (basée sur l’écart-type et la taille de l’échantillon). Finalement, calculez l’intervalle de confiance à 95% basé sur la distribution \(t\):
\[(\bar{x} + t_{(n-1)0.025} s_{\bar{x}}, \bar{x} + t_{(n-1)0.975} s_{\bar{x}})\]
Rappel: La fonction qt(p, df) permet d’obtenir pour une valeur p donnée la valeur du quantile de la distribution \(t\) avec df degrés de liberté.
Réponse
cov_dr <- cover$sphcover[cover$habitat == "Dr"]
n <- length(cov_dr)
# Moyenne
moy <- mean(cov_dr)
moy## [1] 7.16229# Erreur-type
err_type <- sd(cov_dr) / sqrt(n)
err_type## [1] 2.517416# Intervalle de confiance
ic <- c(moy + qt(0.025, n - 1) * err_type,
moy + qt(0.975, n - 1) * err_type)
ic## [1] 1.357118 12.967461- Simulez 10 000 échantillons bootstrap pour la moyenne calculée en a). Quelle est son erreur-type selon le bootstrap? Est-ce que cette statistique apparait biasée?
Réponse
library(boot)
set.seed(5612)
calc_moy <- function(x, i) mean(x[i])
boot_moy <- boot(cov_dr, calc_moy, R = 10000)
# Erreur-type
sd(boot_moy$t)## [1] 2.386784# Biais
mean(boot_moy$t) - boot_moy$t0## [1] 0.0328031Le biais est assez petit (comparé à l’erreur-type) et pourrait être dû à une erreur numérique plutôt qu’à un biais réel de la statistique.
- Comment la distribution du bootstrap diffère-t-elle d’une distribution normale? Pour répondre à cette question, il peut être utile de tracer un graphique quantile-quantile (dans le code ci-dessous,
resest le résultat du bootstrap):
qqnorm(res$t)
qqline(res$t)Réponse
qqnorm(boot_moy$t)
qqline(boot_moy$t)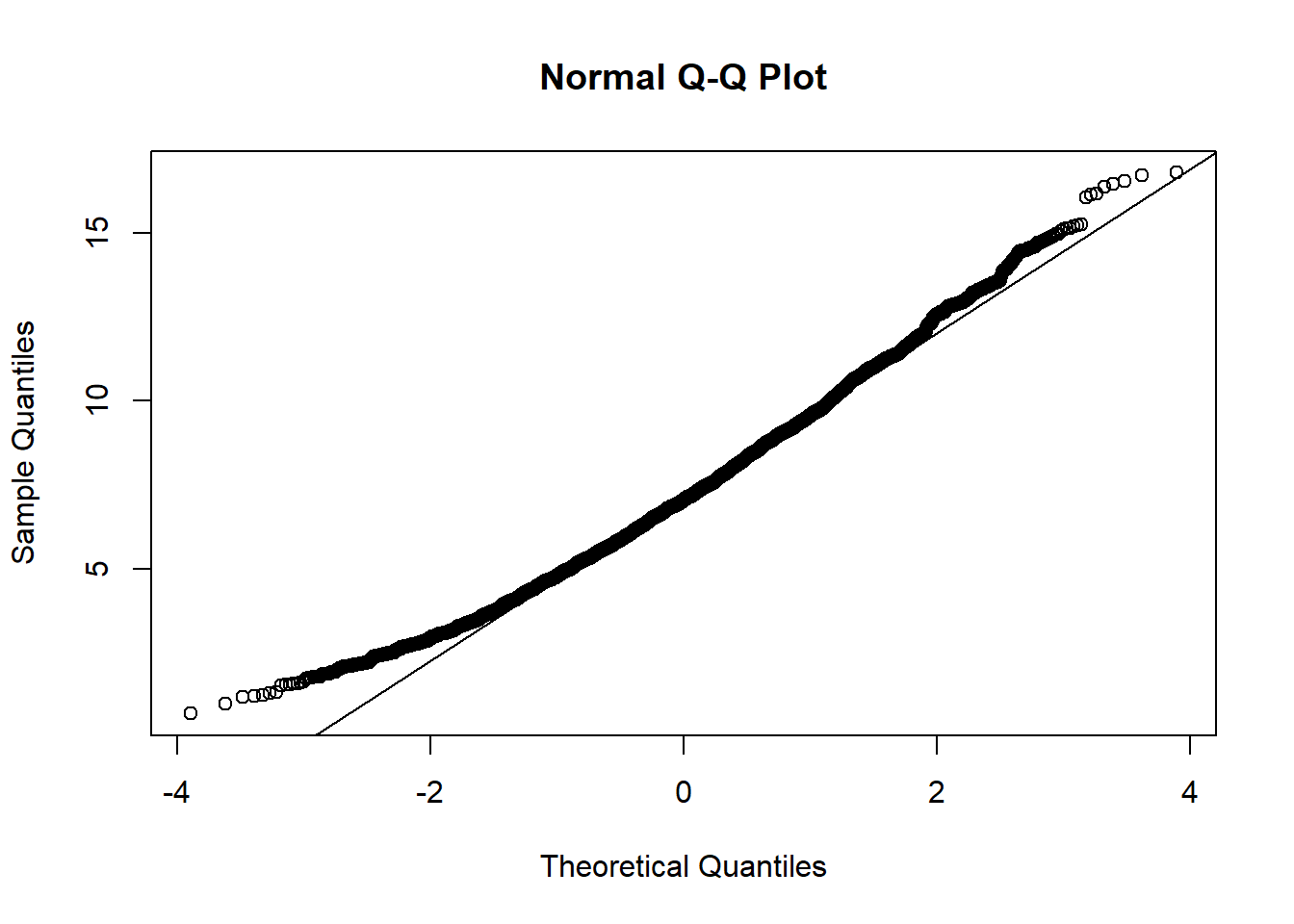
La distribution du bootstrap est asymétrique: les plus petites valeurs sont au-dessus de la droite, donc plus rapprochées de la moyenne comparé à une distribution normale, tandis que les plus grandes valeurs sont aussi au-dessus de la droite, donc elles sont plus éloignées de la moyenne.
- Calculez l’intervalle de confiance à 95% de la moyenne selon la méthode BCa. Comment diffère-t-il de celui calculé en a) selon la formule classique? Pouvez-vous expliquer cette différence en fonction du résultat en c)?
Réponse
# Intervalle de confiance
boot.ci(boot_moy)## Warning in boot.ci(boot_moy): bootstrap variances needed for studentized
## intervals## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 10000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = boot_moy)
##
## Intervals :
## Level Normal Basic
## 95% ( 2.451, 11.807 ) ( 1.985, 11.324 )
##
## Level Percentile BCa
## 95% ( 3.001, 12.340 ) ( 3.430, 13.281 )
## Calculations and Intervals on Original ScaleL’intervalle BCa (3.43, 13.28) diffère de celui en a) (1.36, 12.97) surtout au niveau de la borne inférieure et les deux bornes sont corrigées vers le haut. En c), nous avons vu que les petites valeurs de la distribution du bootstrap sont plus rapprochées de la moyenne par rapport à la distribution normale et les plus grandes valeurs s’en éloignent.
2. Estimation des différences entre habitats
- Voici la distribution des valeurs de sphcover dans chaque type d’habitat.
library(ggplot2)
ggplot(cover, aes(x = habitat, y = sphcover)) +
geom_boxplot()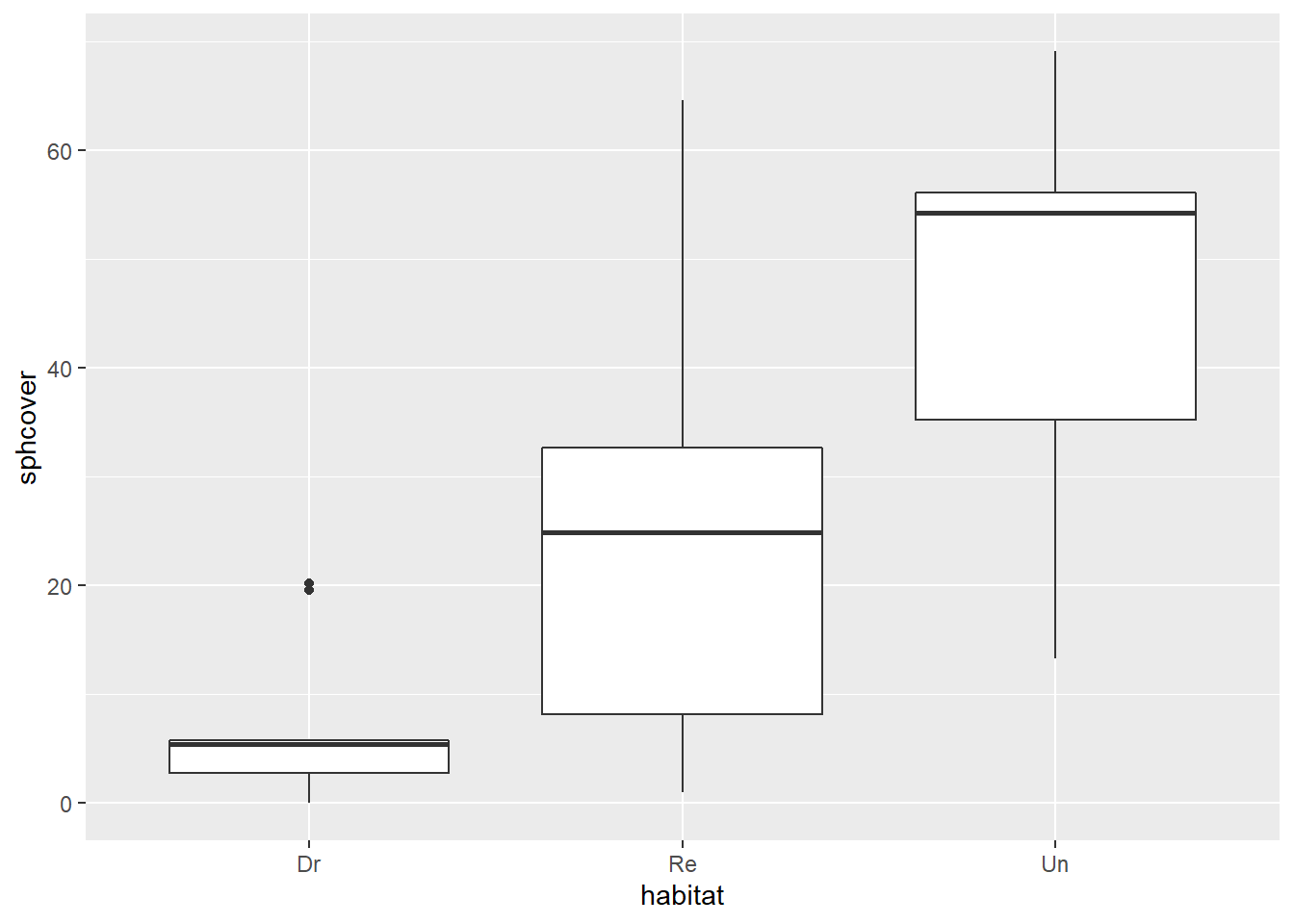
Quelles sont les suppositions d’un modèle d’ANOVA classique qui décrirait la couverture des sphaignes en fonction du type d’habitat? Est-ce que ces suppositions semblent respectées ici?
Réponse
L’ANOVA suppose que les résidus suivent une distribution normale de même variance pour chaque groupe. Ici, les distributions sont asymétriques et la variance du groupe Dr semble plus petite.
- Ajustez le modèle linéaire
sphcover ~ habitatau jeu de donnéescover. Consultez le sommaire des résultats du modèle avec la fonctionsummaryet les intervalles de confiance des coefficients avec la fonctionconfint. Quelle est l’interprétation de chaque coefficient? Les intervalles de confiance sont-ils plausibles?
Réponse
mod <- lm(sphcover ~ habitat, data = cover)
summary(mod)##
## Call:
## lm(formula = sphcover ~ habitat, data = cover)
##
## Residuals:
## Min 1Q Median 3Q Max
## -33.144 -8.161 -0.596 9.659 41.371
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 7.162 5.129 1.396 0.1719
## habitatRe 16.141 6.282 2.569 0.0149 *
## habitatUn 39.266 7.254 5.413 5.45e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 15.39 on 33 degrees of freedom
## Multiple R-squared: 0.4742, Adjusted R-squared: 0.4424
## F-statistic: 14.88 on 2 and 33 DF, p-value: 2.473e-05L’ordonnée à l’origine (Intercept) est la couverture moyenne pour le groupe de référence (marécages drainés, Dr). Le coefficient habitatRe (respectivement, habitatUn) est la différence entre la couverture moyenne des marécages remouillés et celle des marécages drainés (respectivement, la différence entre les marécages non-drainés et drainés).
confint(mod)## 2.5 % 97.5 %
## (Intercept) -3.273495 17.59807
## habitatRe 3.360128 28.92248
## habitatUn 24.507522 54.02438L’intervalle de confiance pour la moyenne du groupe Dr atteint des valeurs négatives, ce qui n’est pas possible pour un pourcentage de couverture.
- Créez une fonction avec pour arguments
xeti, qui ajuste le modèle linéaire en b) en remplaçant le jeu de données original (data = cover) pardata = x[i, ], puis retourne les coefficients du modèle avec la fonctioncoef. Ensuite, appliquezbootau jeu de donnéescoveravec la fonction créée et en effectuant 10 000 réplicats.
Notes
Lorsque le premier argument de
bootest un jeu de données, ce sont les rangées de ce jeu de données qui sont ré-échantillonnées.Puisque la statistique calculée par la fonction comporte plusieurs valeurs (chacun des coefficients), l’élément
tdu résultat debootest une matrice plutôt qu’un vecteur. Les colonnes de cette matrice correspondent à chacun des coefficients dans l’ordre. Vous pouvez calculer une statistique pour chaque colonne avec la fonctionapply, ex.:apply(res$t, 2, mean). Ici,2indique de calculer la fonctionmeanpar colonne (1signifierait par rangée).
Réponse
lm_hab <- function(x, i) {
mod <- lm(sphcover ~ habitat, x[i,])
coef(mod)
}
boot_hab <- boot(cover, lm_hab, R = 10000)
# Moyenne
apply(boot_hab$t, 2, mean)## [1] 7.193903 16.132949 39.288069# Erreur-type
apply(boot_hab$t, 2, sd)## [1] 2.529526 4.599182 6.523183La moyenne du bootstrap est très proche des coefficients estimés en b), mais les erreurs-types ont diminué.
Notons que tous les coefficients dépendent de la moyenne du groupe de référence Dr. La moyenne et l’écart-type de ce groupe sont fortement affectés par deux valeurs extrêmes autour de 20, comme on peut voir sur le graphique en a). Ces valeurs extrêmes seront absentes dans plusieurs échantillons bootstrap, ce qui a pour effet de réduire l’écart-type estimée pour le groupe Dr et ainsi réduire l’erreur-type des coefficients du modèle.
- L’application du bootstrap en c) ré-échantillonne parmi l’ensemble des rangées, ce qui fait que le nombre d’observations dans chaque type d’habitat varie d’un échantillon à l’autre. S’il est préférable de considérer ces nombres comme des quantités fixes, on peut définir les types d’habitat comme des strates en ajoutant l’argument
strata = as.factor(cover$habitat)à la fonctionboot. (La conversion de la variablehabitaten facteur est nécessaire ici.)
Répétez l’analyse en c) avec un ré-échantillonnage stratifié et comparez les erreurs-types obtenues pour chaque coefficient.
Réponse
boot_strat <- boot(cover, lm_hab, R = 10000, strata = as.factor(cover$habitat))
# Moyenne
apply(boot_strat$t, 2, mean)## [1] 7.165948 16.180594 39.323302# Erreur-type
apply(boot_strat$t, 2, sd)## [1] 2.372362 4.490822 6.173863Toutes les erreurs-types ont diminué par rapport à c).
- Calculez l’intervalle de confiance pour le coefficient
habitatUnselon le résultat du bootstrap en d). Notez qu’il faut ajouter l’argumentindex = 3à la fonctionboot.cipour indiquer à R de calculer l’intervalle pour le 3e coefficient.
Réponse
boot.ci(boot_strat, index = 3)## Warning in boot.ci(boot_strat, index = 3): bootstrap variances needed for
## studentized intervals## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 10000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = boot_strat, index = 3)
##
## Intervals :
## Level Normal Basic
## 95% (27.11, 51.31 ) (27.86, 51.77 )
##
## Level Percentile BCa
## 95% (26.76, 50.68 ) (25.24, 49.55 )
## Calculations and Intervals on Original Scale- Finalement, nous allons ré-échantillonner les résidus du modèle.
Ajustez un modèle linéaire comme en b), puis ajoutez au jeu de données
coverune colonne pour les valeurs attendues (fitted) du modèle.Écrivez une fonction qui crée un nouveau jeu de données en additionnant un vecteur ré-échantillonné
x[i]aux valeurs attendues pour produire une nouvelle variable réponse, puis qui ajuste un modèle avec cette nouvelle variable réponse en fonction de l’habitat.Simulez 10 000 échantillons avec la fonction
boot, avec comme arguments (1) le vecteur de résidus (residuals) du modèle et (2) la fonction créée ci-dessus. Ne spécifiez pas de strates. Calculez de nouveau la moyenne, l’erreur-type et l’intervalle de confiance à 95% des coefficients.
Le ré-échantillonnage des résidus est-il un bon choix pour ces données?
Réponse
mod <- lm(sphcover ~ habitat, data = cover)
cover$fitted <- fitted(mod)
lm_resid <- function(x, i) {
cover$cover_new <- cover$fitted + x[i]
mod_new <- lm(cover_new ~ habitat, data = cover)
coef(mod_new)
}
boot_resid <- boot(residuals(mod), lm_resid, R = 10000)
# Moyenne
apply(boot_resid$t, 2, mean)## [1] 7.155993 16.157210 39.340901# Erreur-type
apply(boot_resid$t, 2, sd)## [1] 4.941989 6.059448 6.965119boot.ci(boot_resid, index = 3)## Warning in boot.ci(boot_resid, index = 3): bootstrap variances needed for
## studentized intervals## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 10000 bootstrap replicates
##
## CALL :
## boot.ci(boot.out = boot_resid, index = 3)
##
## Intervals :
## Level Normal Basic
## 95% (25.54, 52.84 ) (25.71, 52.94 )
##
## Level Percentile BCa
## 95% (25.59, 52.82 ) (25.23, 52.53 )
## Calculations and Intervals on Original ScaleLe ré-échantillonnage des résidus suppose que les résidus dans chaque groupe proviennent de la même distribution. Dans ce cas-ci, les variances ne sont pas homogènes entre les groupes, donc il est préférable de ré-échantilonner les observations.