Spruce Budworm Outbreaks
Hierarchical Bayesian models (also known as Bayesian networks) are used to describe complex data-generating process as graphs of random variables, that include observed data but also missing data or latent variables. Variables in the model are connected by relationships of conditional probability and the parameters of those relationships can be estimated by Monte Carlo algorithms such as Markov Chain (MCMC) or Hamiltonian (HMC) Monte Carlo.
This modeling framework is particularly useful for problems involving data fusion, the integration of multiple independent sources of data on a given system to obtain a more precise statistical description of the system. I have used this method for both historical reconstruction and year-to-year forecasting of spruce budworm outbreaks in Quebec, Canada. Outbreaks of this insect occur on a cycle of around 30 years in Eastern Canada, causing defoliation of millions of hectares of spruce and fir forests.
Growth-ring chronologies obtained from tree coring provide long time records of events impacting tree growth, including spruce budworm outbreaks. Previous studies have relied on rule-of-thumb criteria (e.g. loss of X% growth over Y years) for delimiting outbreak periods in growth-ring time series. I have proposed a fully-probabilistic alternative to this method, using a Bayesian network to “calibrate” the tree-ring signal based on direct aerial observation of spruce budworm outbreak intensity during the latter part (1970-present) of the time series ( Conference presentation ).
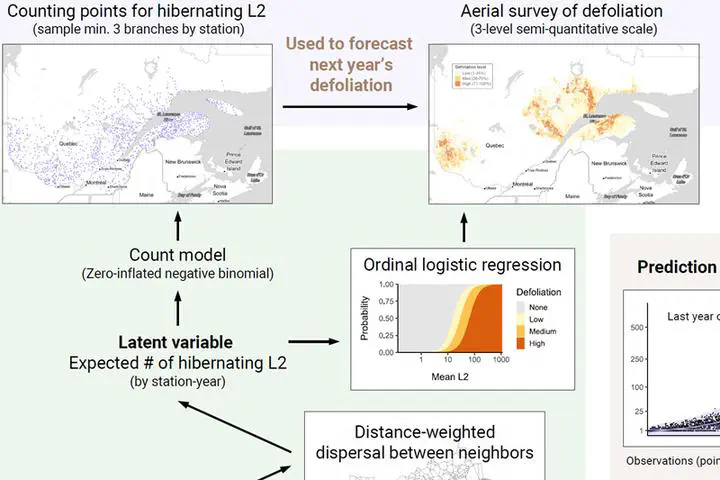
To forecast the evolution of outbreaks, the Quebec forestry authority manages a network of monitoring stations where hibernating spruce budworm larvae are counted on a sample of branches each fall, as a predictor of the next summer’s outbreak intensity. We combined this detailed population data available at a few point locations with a coarser, more widely available measure of outbreak intensity (provincewide aerial surveys conducted during the summer) to estimate the spruce budworm’s population dynamics over the length of the current outbreak (~ 15 years), extend the forecasting horizon from 1 to 2 years, and interpolate the population estimates between the locations of monitoring stations ( Poster ).